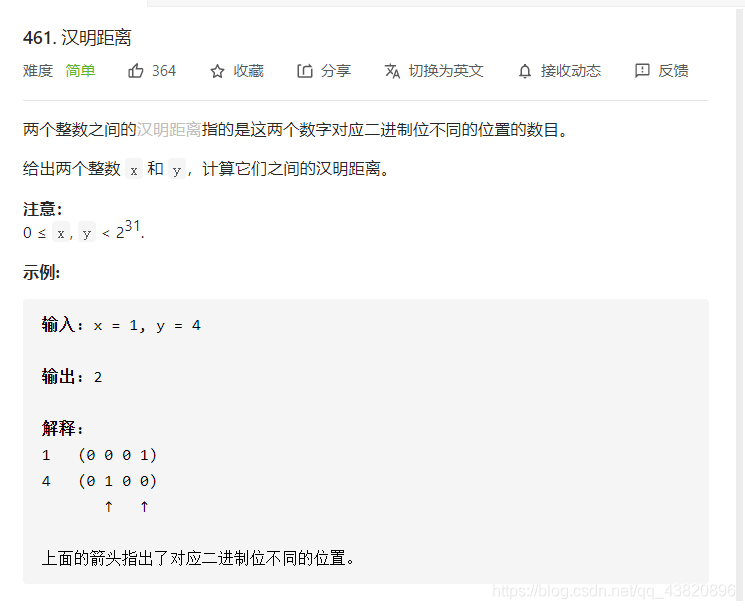
题目描述

一、解题思路

这里有两种解题思路

1. 位运算法

位运算如果你不了解的话，可以看下第二种解题思路。但是整体代码有点冗余，而且效率也不高。
^的运算规则二进制位中各个位上数就是相同为 0，不同为 1。
&的运算规则是都为 1 时结果为 1，反之全为 0。
|的运算规则是只要有 1 结果为 1，反之为 0。
>>当前数二级制向右移一位，同时最高位根据数的正负来补 0 或 1
<< 当前数二进制向左移一位，同时最低位补 0。

位运算法

将两个数^运算
判断运算结果中 1 的个数。即为两个数二进制中各个位的值不同的个数
这里有两种计算 1 个数的方法
2.1.1 将运算结果按 2 求余，如果为 1 就个数加 1。反之就忽略
2.1.2 将运算结果右移一位。并重复上述步骤 32 次。
2.2.1 将运算结果和运算结果-1 进行&运算，然后将值返回作为新的运算结果。1 的个数加 1。
2.2.2 直到运算结果为 0 时跳出循环

2. 暴力破解法

将上述两个数将其二进制位分别放入到不同的 List 容器中
判断两个容器的长度，将长度较大的容器作为遍历次数
获取两个容器中当前索引的值，并判断是否相等，如果不等距离加 1
如果较小容器遍历完了的话，就判断较大容器中的值是否等于 0。如果不等距离加 1
最后得到的距离即为结果

二、代码

1.位运算

public int hammingDistance(int x, int y) {
     int res=x^y;
     int times=0;
   while(res!=0){
       res=res&(res-1);
       times++;
   }
   return times;
 }

2.暴力破解

public int hammingDistance(int x, int y) {
        int i;
       ArrayList<Integer> xArray=new ArrayList<>();
       do{
       xArray.add(x%2);
       x=x/2;
     }while(x!=0);

       ArrayList<Integer> yArray=new ArrayList<>();

     do{
       yArray.add(y%2);
       y=y/2;
     }while(y!=0);



        int distance=0;
       //当y的二进制更长时
       if(yArray.size()>=xArray.size()){
            for (int j=0;j<yArray.size();j++){
                if(j<xArray.size()){
                   if(yArray.get(j)!=xArray.get(j)){
                       distance++;
                   }
                }else{
                    if(yArray.get(j)!=0){
                        distance++;
                    }
                }
            }
       }else{//x的二进制更长
            for (int j=0;j<xArray.size();j++){
               if(j<yArray.size()){
                   if(yArray.get(j)!=xArray.get(j)){
                       distance++;
                   }
                }else{
                    if(xArray.get(j)!=0){
                        distance++;
                    }
                }
            }
       }

       return distance;
   }